Hello, and welcome to the Tips for Teachers newsletter.
I have 7 free websites
I write 2 free weekly newsletters
I host 2 free podcasts
I share over 200 free CPD videos
If you find my work useful, please consider becoming a Patreon
💡 A tip to try in class this week 💡
A follow-up question is a key feature of my model of responsive teaching. If we have evidence that understanding is not secure, a clear teacher explanation, followed by a re-check for understanding using a question that assesses the same skill, provides much more reliable evidence that our response has had the intended impact than the classic: Does that make sense?
Many maths teachers I work with are tempted to create this follow-up question on the spot. This saves planning time, and sometimes they get away with it. But there are two reasons why I think this is a risky strategy:
You might make up a bad question
A teacher I observed recently asked the following diagnostic question:
Students struggled, so the teacher explained why the correct answer was D. He then made up a follow-up question on the spot to re-check his students’ understanding:
Do you see the problem? One of the critical misconceptions students have about the laws of indices is knowing whether to add or multiply the powers. With a 2 and 2, you can do it either way and still be correct.
Or how about this one? A teacher asked the following question:
The mistake several students made was not to factories enough:
So the teacher modelled the solution, and then made up a question to check students’ understanding:
But of course, the question does not test that same mistake as 5 and 25, which do not have any other common factors.
In the heat of a lesson, with many things vying for our limited attention, the chance of us making up as good a follow-up question as we would outside this environment is minimal.
You might not be able to think of a follow-up question
Students struggled with the subtracting fractions question, so the teacher made them up a follow-up question on the spot:
But they also struggled with this question:
So what did the teacher do following his explanation? Ask them “Does that make sense?”.
In the coaching session afterwards, I asked him why he did a follow-up question for the fractions question but not one for the Venn Diagrams question. He replied, “Because I couldn’t think of a Venn Diagram question in the moment.”
But when planning the lesson, he could have.
Conclusion
Creating a follow-up question on the spot may be tempting. But for an extra couple of minutes of planning time, I recommend preparing it in advance. It ensures that you have a question to ask and that the data you get about your students’ understanding will be more reliable.
What do you think of this idea?
What would you need to change to make this tip work for you?
When could you try it for the first time?
View more than 200 Tips for Teachers
🏃🏻♂️Before you go, have you… 🏃🏻♂️
… tried last week’s tip about sometimes not using mini-whiteboards?
… read my latest Eedi newsletter about Silent Teacher?
… listened to my latest podcast with Kris Boulton about Atomisation?
… read my Tips for Teachers book?
… considered booking some CPD, coaching or maths department support?








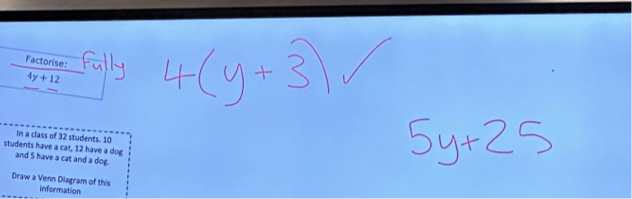


Yes, plan follow up questions ahead of time. But, make sure your follow up question makes sense before asking it.
In an English class I took in college, the teacher wanted us to compare Lao Tzu to Machiavelli to give us the idea that Lao Tzu was an optimist and Machiavelli a pessimist. I explained why I thought that was missing the point of Machiavelli, and probably Lao Tzu as well, but he had a script he wanted to follow and my observation did not fit it. He ignored my remarks and asked his planned follow up questions, solidifying for us the optimism and pessimism of the writers.
Weeks later, upon studying both more in depth, the teacher was excited to break our perspectives that the writers were optimistic or pessimistic, explaining this new alternative interpretation I had already come to on my own and was shut down for.
Having planned follow up questions is helpful, but having a railroaded script is not. The danger is whether you're listening to understand or listening to respond. I'm sure, depending on the subject, this may not be a point of concern. For math, it's probably much more straightforward. But certain teachers may want to be more careful here.