Hello, and welcome to the Tips for Teachers newsletter.
I have 7 free websites
I write 2 free weekly newsletters
I host 2 free podcasts
I share over 200 free CPD videos
If you find my work useful, please consider becoming a Patreon
💡 A tip to try in class this week 💡
One of the many ideas I took from my podcast conversation with Kris Boulton is the idea of overtisation. Put simply, this means making invisible steps visible to our students, especially when they initially encounter an idea.
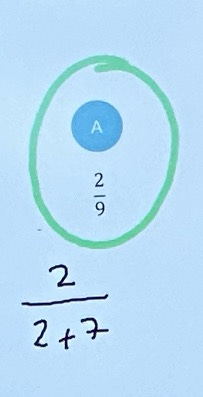
I saw a really nice example of overtisation during a recent school visit. The teacher was using a diagnostic question to check students' understanding of writing fractions as ratios.
The correct answer was A, but can you see what the teacher did underneath? He made it super-explicit exactly where the denominator, 9, had come from by showing it is the sum of the two parts, 2 and 7. Now, most teachers would have mentioned this when explaining the answer, but how many would have written it? I am not sure I would have. But by doing so, we significantly increase the chance of our students seeing exactly where the answer comes from.
Other examples of overtisiation in maths are:
Writing 1x instead of x to show explicitly what the coefficient is
Writing a multiplication sign outside a bracket ready to be expanded to show exactly what operation we need to do
Writing 3x^2 - 4x = 0 as 3x^2 - 4x + 0 = 0 when using the quadratic formula to make it clear exactly what the value of c is
What I find interesting about overtisation is that I actively tell students not to do many of the examples above as they are “not the way a mathematician writes”. But in the initial stages of learning a concept, an insistence upon potentially confusing conventions like these is likely to hinder learning. Those conventions can be introduced later - a process known as covertisation - when shortcuts can be made in the name of both convention and efficiency.
Be on the lookout for opportunities to overtise, and thus make invisible steps visible.
What do you think of this idea?
What would you need to change to make this tip work for you?
When could you try it for the first time?
View more than 200 Tips for Teachers
🏃🏻♂️Before you go, have you… 🏃🏻♂️
… tried last week’s tip about improving data collection with mini-whiteboards?
… read my latest Eedi newsletter about dealing with questions with multiple correct answers?
… listened to my most recent podcast with Kris Boulton about Atomisation?
… read my Tips for Teachers book?
… considered booking some CPD, coaching or maths department support?



Thank you for giving me a name for this - I have a habit of spelling this out for specific students when working 1-1. It can be really powerful.
As a "professional mathematician", what I've found that that even us professional mathematicians do certain steps more overtly than needed because it works better in our brains. For example, I find calculating a/b-1 to be tricky, so I write it as a/b - b/b = (a-b)/b to make it obvious for myself. That's not "cheating" or being "stupid". It's working efficiently. The reason it's not second nature for me is because most of the time I'm writing Matlab scripts to do it for me :-)
Craig! Oh man! You took me back to my high school days and math class! I learned a new word today by the way!
I wish that my math teachers would have done this especially after going through exam answers and just making it obvious because I think this speaks to the fact that teachers can have the access to be able to connect the different ways students learn to any activity. Like this would be perfect for a visual learner like myself rather than the teacher just saying it!
Really cool stuff! Can't wait to follow along! I just subscribed!